Modeling the Debate Flow

In the world of high-level policy debate, the air is often filled with “spread,” the practice of speaking at upwards of 300 words per minute to maximize the density of arguments. To an outsider, it sounds like a chaotic blur of rhetoric and adrenaline. However, beneath this high-velocity exterior lies a rigid, almost mechanical system of logical dependencies. A Disadvantage (sidenote: An argument brought up by the negative team highlighting the consequence resulting from the passage of the plan.) collapses if its Uniqueness (sidenote: Evidence describing the current state of affairs (or the status quo)) is proven false; an Impact (sidenote: The consequence of the disadvantage or the benefit of an affirmative plan. They are often quite catastrophic or extreme, such as nuclear war, economic collapse, pandemics, etc.) vanishes if the Internal Link (sidenote: The logical chain connecting the argument to its impact. It bridges, for example, a policy causing economic decline (link) with that decline leading to war (impact).) chain is severed. Debaters have long navigated these structures through intuition and “flow” (the shorthand notation used to track the round). But what happens when we stop treating a debate as a speech contest and start modeling it as a formal mathematical object?

Arguments as a Directed Graph

To analyze the structural integrity of a debate, we must first abstract away the prose and focus on the logic. We can represent a debate round as a directed graph \(G = (V, E)\), where each node \(v \in V\) represents an argument represents an argumentative unit: a claim, a warrant, a link, or an impact. The edges E represent the dependencies between these units. For example, if Node A is “Plan saves the economy” and Node B is “Economic stability prevents war,” an edge \(A \rightarrow B\) indicates that the truth of B in the context of the round is dependent on the truth of A.

By defining the round this way, we shift the focus from what is being said to how it is connected. In this model, nodes carry specific attributes: intrinsic probability (the strength of the evidence), magnitude (the size of the impact), and direction (a polarity of +1 for Affirmative support or -1 for a Negative “turn”). This formalization allows us to move beyond simple “if-then” statements and toward a system where we can calculate the “activation strength” of an argument based on its upstream dependencies.

Building the Engine from Scratch

While libraries like networkx (sidenote: A well known Python package for the creation, manipulation, and study of complex network structures (graphs).) offer high-level abstractions, I chose to implement the core graph engine from scratch in Python to maintain total control over the propagation logic. Using an adjacency list representation, I implemented fundamental algorithms including a Depth-First Search (DFS) for cycle detection and a topological sort to ensure that probability “flows” correctly from root nodes (Uniqueness) to leaf nodes (Impacts).

class Node:
    def __init__(self, uid, name, node_type, prob=1.0, mag=0.0, direction=1):
        self.uid = uid
        self.name = name
        self.node_type = node_type # uniqueness, link, impact
        self.prob = prob           # intrinsic probability
        self.mag = mag             # impact magnitude
        self.direction = direction # +1 for AFF, -1 for NEG
        self.activation_score = 0.0

The engine relies on a custom propagation function. For any given node, its activation score is not just its own probability, but a product of all necessary upstream links. For independent paths leading to the same impact, I implemented an “OR” logic gate based on independent probabilities:

$$ P(A \cup B) = 1 - (1 - P(A)) \times (1 - P(B)) $$

or

$$ P(Impact) = 1 - \prod_{i=1}^{n} (1 - P(Link_i)) $$

This ensures that the model respects “multi-point” links while still penalizing the “link-chain decay” common in long, complex arguments.

Sensitivity and Fragility

The true value of a structural model lies in its ability to handle perturbations. By simulating the “concession” of an argument, setting a node’s probability to zero, we can observe the systemic collapse of an entire position. This led to the development of a “Fragility Metric.” We define the fragility of a node as the absolute change in the total expected impact of the round if that node were to be removed.

To test the model, I simulated a standard Economic Disadvantage. The baseline graph showed a high-magnitude negative impact. However, by introducing a “Link Turn” with a polarity-reversing edge, the engine successfully re-calculated the flow, showing that the “Global War” impact had been mathematically captured by the Affirmative.

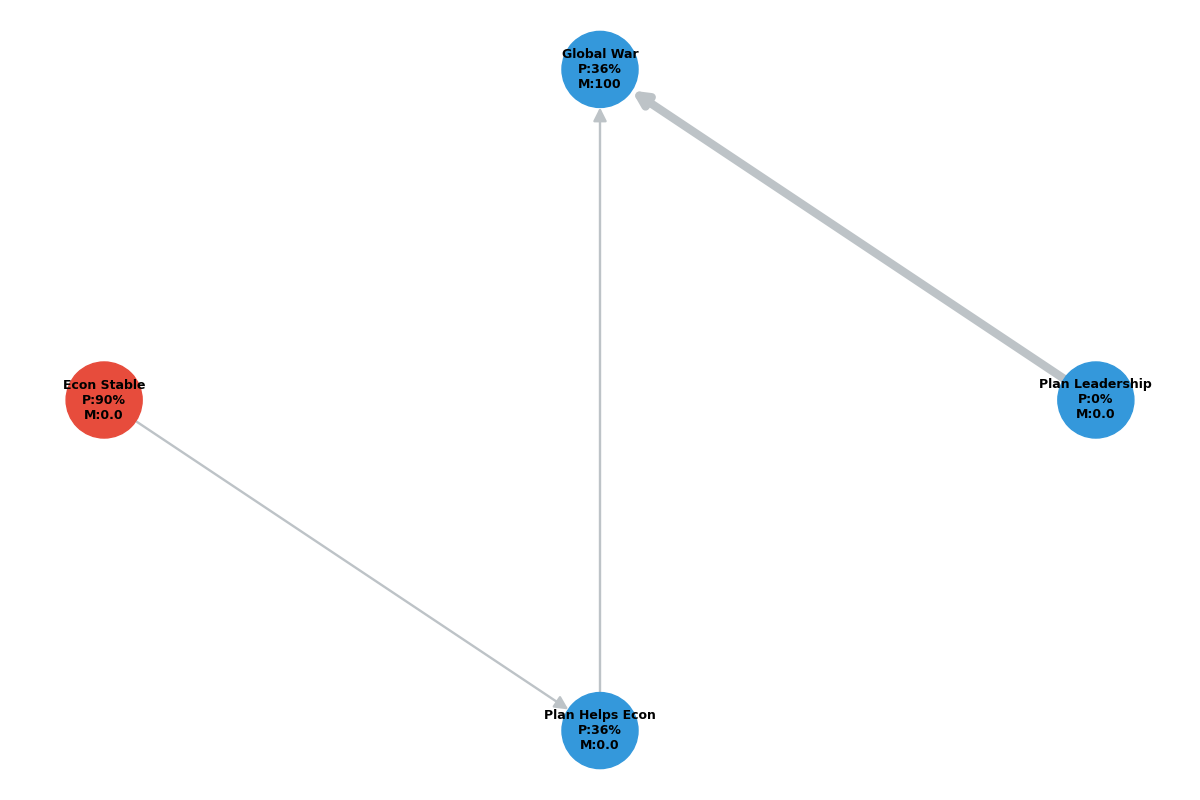
A subsequent sensitivity analysis revealed that the internal link was the most fragile point in the chain. While debaters often spend the most time arguing about the magnitude of the impact, the model demonstrated that a small 20% shift in the link’s probability resulted in a 60% reduction in the total expected risk. This highlights a common strategic error: over-investing in impact rhetoric while neglecting the structural bottlenecks of the link chain.

The Monte Carlo Simulation

Real-world reasoning is rarely binary, it’s usually stochastic. To account for the uncertainty of a judge’s perception, I implemented a Monte Carlo simulation. Rather than assuming a link is exactly 60% likely, we assign it a confidence interval (a standard deviation \(σ\)). By running 1,000 simulated “universes,” the engine generates a distribution of potential outcomes rather than a single win/loss result.

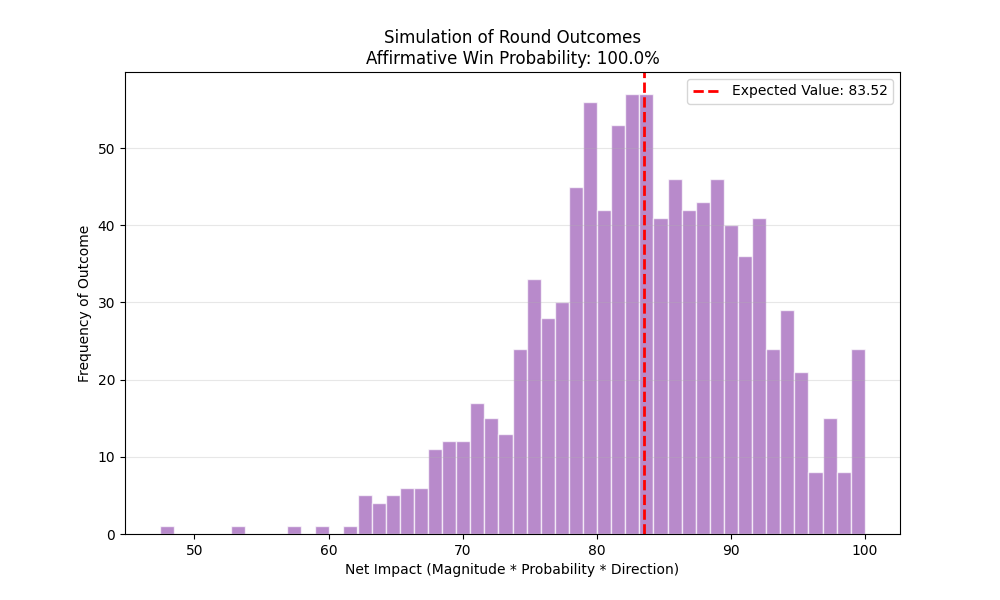
The resulting histogram provides a “Win Probability” for each side. A narrow, tall spike suggests a structurally sound case where the outcome is predictable. A wide, flat distribution suggests a “messy” round where the outcome is highly volatile and dependent on minor fluctuations in how specific links are perceived. This transforms the post-round critique from a subjective narrative into a data-driven post-mortem of logical risk.

Reflections and Questions

Formalizing a debate round as a directed graph reveals a fundamental truth about adversarial reasoning: complexity is a liability. In our simulations, “long” link chains—even those with high-probability individual nodes—consistently showed higher fragility and lower expected value than “short” but robust arguments. This suggests that in systems of high uncertainty, structural simplicity is a strategic imperative.

Moving forward, I am interested in exploring recursive logic. While this engine handles Directed Acyclic Graphs (DAGs) well, real-world “theory” arguments often create logical loops (e.g., Argument A is true only if the rules governing Argument A are valid). Modeling these cycles without infinite recursion requires a more complex state-machine approach.

How might we model “judge intervention” as a weight-bias in the graph? If a judge has a 5% bias against a certain type of argument, does that bias propagate linearly or exponentially through the link chain?

Open Source

I’ve open-sourced the code on GitHub. Feel free to reproduce the experiments, test different graph structures, and explore the strategic implications of fragility in adversarial reasoning. I think it’s a cool experiment that anyone interested in debate, logic, or in systems thinking might find insightful.